“Those numbers are skewed.” “That survey is biased.” “Heresy!” These are explanations we’ve all used to excuse away numbers proving our theory or belief to be incorrect. While our skepticism is usually justifiable given the ease with which data can be manipulated and repackaged, we still don’t know when or why to believe in statistical results.

These same responses to unpopular statistics can often be heard coming from the mouths of website data analysts. Other than, “the tracking code didn’t fire correctly,” one of the most common web analyst defenses might be, “but it’s not statistically significant.” Given the general distaste among the marketing community for anything suggesting scientific leanings, these rationalizations are usually accepted without further comment or debate.

What’s interesting about this particular self-defeatism is that by refusing to delve into what the numbers mean, CMOs and even CEOs are handing control of their marketing efforts over to a data analyst who may not even know what their goals are.

Now, I will admit, the exhortation above is a dramatization coming from years of people dismissing or ignoring evidence of statistical relevancy in the data we present to them. Ninety-nine percent of the time you can trust that the data you’re given is valid (I couldn’t resist). The big BUT in this situation is CRO results.

Half the time clients don’t understand what CRO tests are meant to do and are much less able to appreciate nuanced results. Don’t get me wrong, I know for a fact that there are reputable agencies using strong data analysis to develop and run tests yielding critical results that help improve conversion rates as they’re meant to. I also know for a fact that there are agencies perfectly happy to recommend changing the color of a button without a single glance at website metrics.

At the end of the day both methodologies are equivalent as long as the test indicates one variant as superior, right? Wrong, because the true definition of a “meaningful difference” is not the same as the one frequently conferred on it.

CRO tests—everybody wants them. At their base, two variations of a landing page are produced with traffic directed to both in an effort to determine which generates more conversions. So far the complexities have largely been contained within how to determine what test to run, how many tests to run and how long to run said tests.

However, an examination of who is taking the tests is long overdue. The “meaningful difference” between conversion rates that typically serves as the sole factor determining the “winner” of a CRO test is often extremely biased. Frequently, particular pages will be trafficked by visitors that constitute a small proportion of overall visitors but that convert much more highly than the site average. Statistical significance realistically doesn’t justify much when used as an arbitrary threshold established to make you confident when you cross it.

In CRO tests, statistical significance is typically established on a frequentist approach, usually using some sort of t-test or z-score to determine that the percentage of people that visits the site perform the action you are interested in X percentage of times, and, therefore, the test with the higher “X” is the best. Quite often analysts recommend that a test be run for a longer period of time if the page has low traffic to increase the sampling size.

For example, if 10/100 people converted, you would have a conversion rate of 10%, which would be the same if 100/1000 people converted. Very simplistically, the second test is superior because you have a larger number of data points from which to draw an inference, and you can be more certain that your inference is correct. Frequentist theory is commonly used in A/B testing particularly due to the simplicity of comparing results.

However, there are a few problems. First of all, you have to determine the amount of data that you’re going to collect to determine statistical significance before you start the test. That’s fine if your visitors all act the same way, but you run into problems if the first 1,000 visitors perform one way, but visitor 1,001 establishes a new pattern and you have predetermined the sampling size to be 1,000 visits.

Now, you might be thinking, “Okay, easy solution. I’ll just set my sampling size so absurdly high that I’ll capture all possible behaviors.” Again, in theory this seems logical until the methodology behind a frequentist approach is truly examined. Unfortunately, by repeatedly applying a percentage based test across multiple categories of data you end up with a Type I error.

Although the name is innocuous enough, a Type I error results in the rejection of a null hypothesis. Essentially, the test will indicate that a relationship exists when it really doesn’t, like your test being awesome and people converting all the time. A prime example that you can see for yourself of the issue with using frequentist theory for CRO tests is the tendency for any test that is run longer to show a higher likelihood of converting. Did you think that visitors just got used to it and decided they liked it? Not statistically likely. It’s more probable that you have a Type I error.

So, maybe I’ve convinced you that frequentist theory is not for you, leaving you to ask, “What’s left?” The answer is Bayes theorem, and it’s been around a long time.

First developed to explain beliefs, Bayesian probabilities received wider adaptation with the use of computers by being applied to complex problems with multiple data inputs—similar to CRO tests. The background is pretty fascinating, and if you’d like to learn more, I’ve included some articles here, here, and here. If you want the short version, probability is used to measure a proportion of outcomes. This site has quite honestly the most intuitive and direct explanation I could find, which I adapted for our own example. Many kudos.

If you’ve done any research here, you know that there is a famous explanation using breast cancer. Quite honestly, I find that morbid and in an effort to stop promoting statistics I think were arbitrarily picked but relate to the deaths of women, I’m making my own example!

Here’s the setup: Every time a conversion fails or succeeds given the desired conversion action and CRO test set up, additional evidence for or against that particular design is produced. By using the assumption that X percent of people convert for test A, and X percent for test B, and including the subjectivity of visitor intent as well as a probability distribution of 0-100%, then each conversion attempt/failure narrows the estimation of success/failure by a precise amount.

Here comes Bayesian application. By adding a prior probability distribution for X, you can determine how and why the new design performs better/worse much more precisely. So you would know, for example, that highly converting blog traffic is causing a skewed result leading to a test being preferred rather than assuming that a test being preferred means it was always more successful. An extrapolation of this would be calculating the expected value of knowing test A is worse than test B, but becoming even more sure would be worth the loss of conversions.

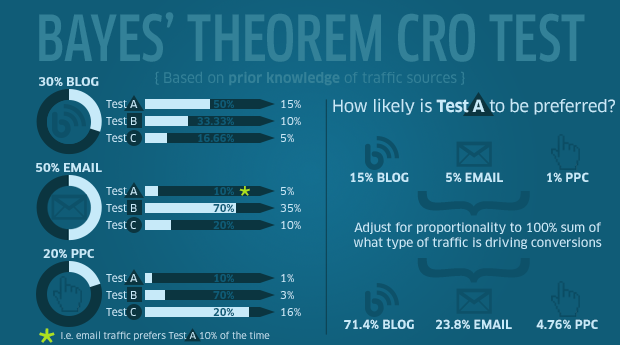
And here’s my data illustrating how this works:

So, by knowing that Blog is 30% of traffic, Email is 50% and PPC is 20%, we have established our prior probabilities. We then use the likelihood that a particular test will be preferred. For example, blog traffic prefers test A 50% of the time, combined with a 30%  share of blog traffic in overall traffic, means that 15% of the time for overall traffic Test A is preferred.

Continuing with the test A example, if Test A is preferred through Blog traffic 15% of the time, Email 5% and PPC 1%, we can figure out what type of traffic most prefers one test or the other by adjusting the proportionality sum to 100%. Assume that now Blog preference is 71.4%, Email is 23.8%, and PPC is 4.76%.

We can now confidently state that the preference for Test A is 71.4% due to visitors arriving from the blog. By including the value of Blog conversions, we can anticipate if a test that converts more highly for blog users might be more valuable than a highly converting PPC test.

Even though I love numbers, I’ll be the first to admit that Bayesian inferences are not necessary for every CRO test you run. If, however, you are looking for substantiating evidence that your CRO tests are producing meaningful results, or you are dealing with vast quantities of data that need partitioning for relevant analysis, or you just have a lot of free time, Bayesian applications are your solution. Adding interpretation may be time consuming, but if you get a raise from the extra money your client makes from conversions, it’s well worth it.